全新的神经网络结构——Kolmogorov–Arnold Networks（KAN）

【新智元导读】无需怀念MLP，新网络KAN基于柯尔莫哥洛夫-阿诺德定理，带着更少的参数、更强的性能、更好的可解释性来了，深度学习架构革新进入新时代！

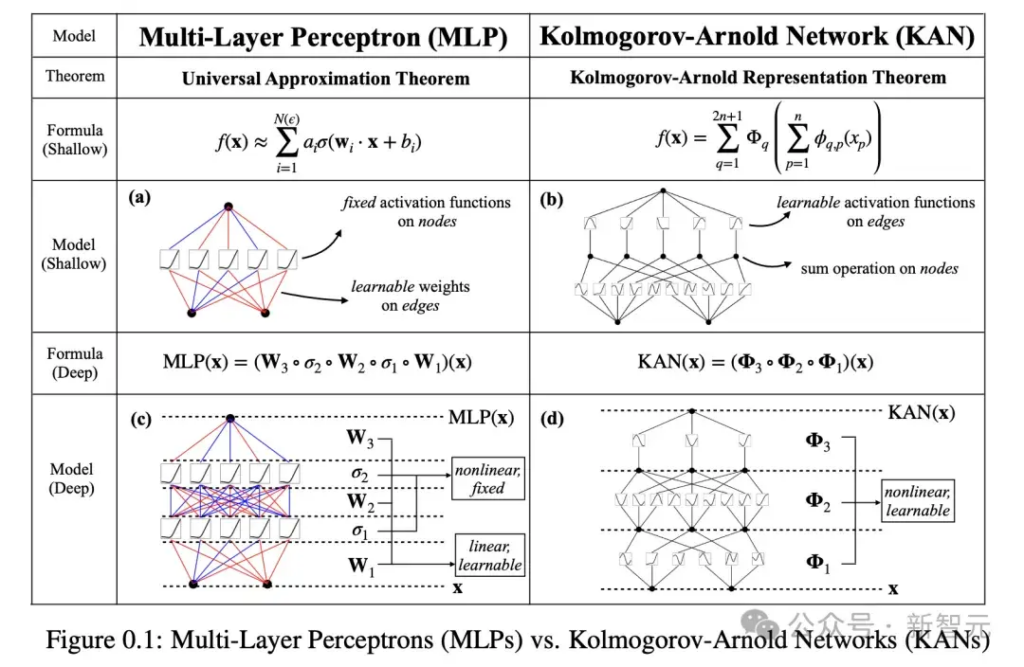
当今，统治深度学习领域的基础架构便是，多层感知器（MLP）——将激活函数放置在神经元上。

那么，除此之外，我们是否还有新的路线可走？

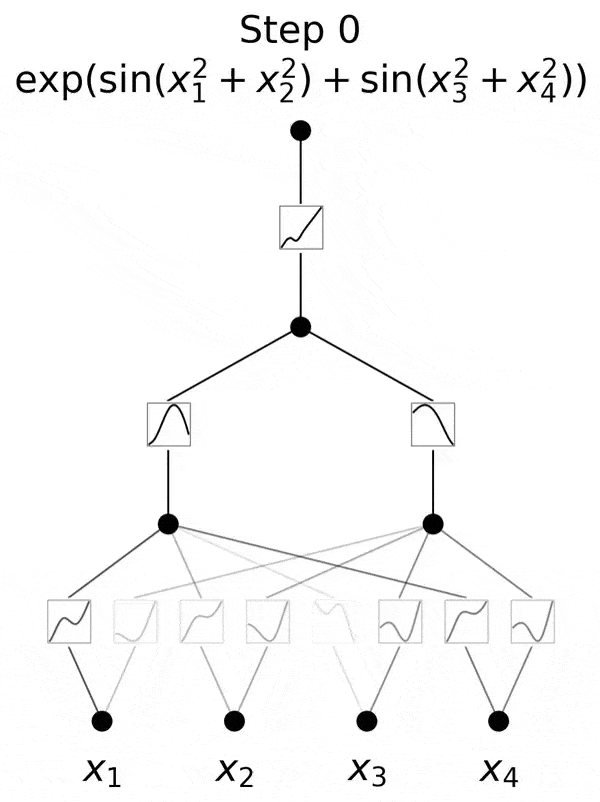
研究人员对MLP做了一个简单的改变，即将可学习的激活函数从节点（神经元）移到边（权重）上！

论文地址：https://arxiv.org/pdf/2404.19756

1）KAN的数学原理：KART定理

KAN的全称是Kolmogorov–Arnold Network，致敬了两位伟大的已故数学家，其背后的核心思想是Kolmogorov–Arnold表示定理，即KART（Kolmogorov–Arnold Representation Theorem）。

KART的核心思想是：对于任何一个多元连续函数，都能够表示为有限个单变量函数和加法的组合。

数学定理读起来比较拗口，但如果把它图示化出来，就很容易弄懂。

假设有一个多元连续函数y=f(x1,x2)，它可以表达为一个有着2个input（x1和x2）、一个output（y）、以及5个隐藏层神经元的Kolmogorov Network。隐藏层神经元数量为2n+1=5，这里的n指的是input变量的个数。

对于第一个神经元，它接收到两个branch的信号，分别是φ1,1(x1)和φ1,2(x2)，这里的φ(xi)是xi的一元函数。把φ1,1(x1)和φ1,2(x2)简单相加，就得到第一个神经元的取值。

以此类推，第2-5个神经元也是如此，这是第一层神经元取值的计算方法。

为了计算第二层神经元的结果，我们需要对第一层中的每个神经元构造一元函数（Φ1到Φ5），然后相加。

这里无论是第一层的函数（小φ）还是第二层的函数（大Φ），都是一元函数，所以可以用曲线将其可视化的表达出来。

至此，我们将f(x1,x2)的KART表示，转化成了一个两层KAN网络，并且进行了可视化。

AI Times